Jupyter interface

Introduction

In a Jupyter notebook, import the TreePPL package and load its extension for Jupyter. This extension provides an easy-to-use interface for working with TreePPL directly within Jupyter notebooks:

import treeppl
%load_ext treeppl.ipython

Once the extension is loaded, you can use the %%treeppl cell magic to write and compile a TreePPL program. Executing the cell creates a treeppl.Model object, which allows interaction with the compiled program directly in Python. This object is stored in a Python variable specified as an argument to the %%treeppl magic (i.e., immediately following %%treeppl on the first line). Optionally, the variable name can be followed by parameters and values. Examples are provided below.

The following cell demonstrates a simple TreePPL program for simulating the flip of a fair coin:

%%treeppl flip samples=10

model function flip() => Bool {
  assume p ~ Bernoulli(0.5);
  return p;
}

In this example, a treeppl.Model instance is created, and the program is compiled. The name flip (specified after %%treeppl) provides an interface for interacting with the model. The argument samples=10 specifies the number of samples to collect when the program is executed.

To run the TreePPL program, simply call the variable as a function (e.g., flip()). This executes the program and returns a treeppl.InferenceResult object, which includes a samples attribute containing the generated samples. While samples may have different weights in more complex programs, they are equally weighted in this simple example. We will cover programs with weighted samples later.

Here’s an example of how to use the compiled program:

res = flip()
res.samples

[True, False, True, False, False, False, False, False, True, True]

Examples from the paper

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import clear_output
from Bio import Phylo

sns.set_theme()

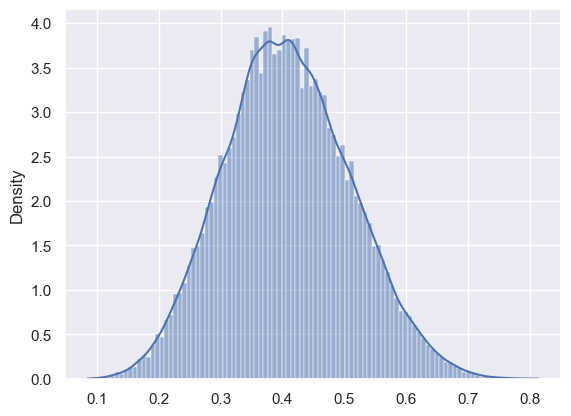
Unfair coin

%%treeppl coin samples=100000

model function coin(outcomes: Bool[]) => Real {
  assume p ~ Uniform(0.0, 1.0);
  for i in 1 to (length(outcomes)) {
    observe outcomes[i] ~ Bernoulli(p);
  }
  return p;
}

res = coin(
    outcomes=[
        True, True, True, False, True, False, False, True, True, False,
        False, False, True, False, True, False, False, False, False, False,
    ]
)
sns.histplot(
    x=res.samples, weights=res.nweights, bins=100, stat="density", kde=True
)

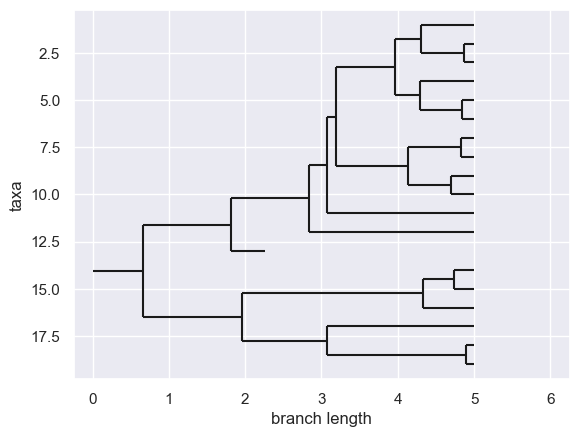
Generating a CRBD tree

%%treeppl generative_crbd samples=1

model function generativeCrbd(time: Real, lambda: Real, mu: Real) => Tree {
  assume waitingTime ~ Exponential(lambda + mu);
  let eventTime = time - waitingTime;
  if eventTime < 0.0 {
    return Leaf {age = 0.0};
  } else {
    assume isSpeciation ~ Bernoulli(lambda / (lambda + mu));
    if isSpeciation {
      return Node {
        left = generativeCrbd(eventTime, lambda, mu),
        right = generativeCrbd(eventTime, lambda, mu),
        age = eventTime
      };
    } else {
      return Leaf {age = eventTime};
    }
  }
}

params = {
    "time": 5.0,
    "lambda": 1.0,
    "mu": 0.1
}

result = generative_crbd(**params)
tree = result.samples[0]
tree = Phylo.BaseTree.Clade(
    branch_length=params["time"] - tree.age,
    clades=[tree.to_biopython()]
)
Phylo.draw(tree)

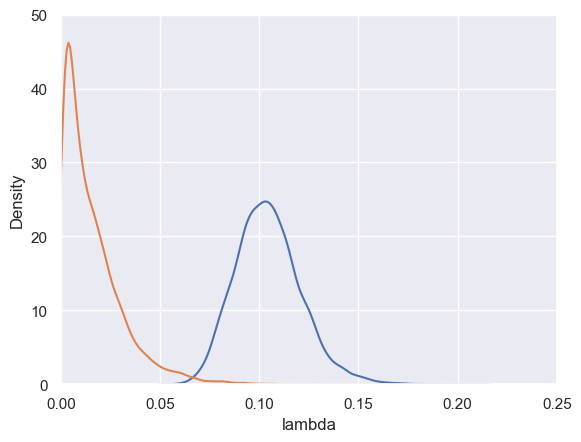
Inferring parameters of a CRBD model

%%treeppl crbd samples=10000 subsamples=10

function simulateExtinctSubtree(time: Real, lambda: Real, mu: Real) {
  assume waitingTime ~ Exponential(lambda + mu);
  if waitingTime > time {
    weight 0.0; resample;
  } else {
    assume isSpeciation ~ Bernoulli(lambda / (lambda + mu));
    if isSpeciation {
      simulateExtinctSubtree(time - waitingTime, lambda, mu);
      simulateExtinctSubtree(time - waitingTime, lambda, mu);
    }
  }
}

function simulateUnobservedSpeciations(node: Tree, time: Real, lambda: Real, mu: Real) {
  assume waitingTime ~ Exponential(lambda);
  if time - waitingTime > node.age {
    simulateExtinctSubtree(time - waitingTime, lambda, mu);
    weight 2.0;
    simulateUnobservedSpeciations(node, time - waitingTime, lambda, mu);
  }
}

function walk(node: Tree, time:Real, lambda: Real, mu: Real) {
  simulateUnobservedSpeciations(node, time, lambda, mu);
  observe 0 ~ Poisson(mu * (time - node.age));
  if node is Node {
    observe 0.0 ~ Exponential(lambda);
    walk(node.left, node.age, lambda, mu);
    walk(node.right, node.age, lambda, mu);
  }
}

model function crbd(tree: Tree) => Real[] {
  assume lambda ~ Gamma(1.0, 1.0);
  assume mu ~ Gamma(1.0, 0.5);
  walk(tree.left, tree.age, lambda, mu);
  walk(tree.right, tree.age, lambda, mu);
  return [lambda, mu];
}

alcedinidae = treeppl.Tree.load("trees/Alcedinidae.phyjson", format="phyjson")

samples = None
for i in range(1000):
    try:
        res = crbd(tree=alcedinidae)
        samples = pd.concat([
            samples,
            pd.DataFrame({
                "lambda": res.items(0), "mu": res.items(1), "lweight": res.norm_const
            })
        ])
        weights = np.exp(samples.lweight - samples.lweight.max())
        clear_output(wait=True)
        sns.kdeplot(data=samples, x="lambda", weights=weights)
        sns.kdeplot(data=samples, x="mu", weights=weights)
        plt.xlim(0, 0.25)
        plt.ylim(0, 50)
        plt.pause(0.05)
    except KeyboardInterrupt:
        break